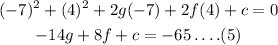Given the points on a circle,
(-5,6),(-3,4),(-7,4),(-5,2)
The general equation is circle is given by,
![\begin{gathered} x^2+y^2+2gx+2fy+c=0\ldots\ldots.(1) \\ \text{radius (r)=}\sqrt[]{g^2+f^2-c} \\ \text{centre (O)=(-g,-f)} \\ \text{Centre radius form is } \\ (x-h)^2+(y-b)^2=r^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/cp8xqs6z6ofiur12lwl9vjzki4mawnykmt.png)
For point (x,y)=(-5,6) the equation of circle becomes,
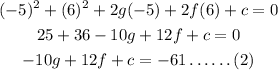
For point (x,y)=(-3,4) the equation of circle becomes,
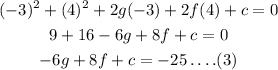
For point (x,y)=(-5,2) the equation of circle becomes,
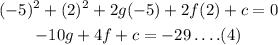
For point (x,y)=(-7,4) the equation of circle becomes,