Question

Suppose AB has length of 6 units and the coordinates of A are (-2,5) Give coordinates for three possible locations for B and the midpoint of each of those possible segments #7 help

Answer 1

Remember that

the distance between two points is equal to

`d=\sqrt[\square]{(y2-y1)^2+(x2-x1)^2}`

In this problem we have

d=6 units

A(-2,5)

B(x,y)

substitute the given values in the expression above

`6=\sqrt[\square]{(y-5)^2+(x+2)^2}`

squared both sides

`36=(y-5)^2_{}+(x+2)^2`

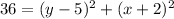
Find out three possible coordinates of point B

First and Second possibles coordinate

I will assume the x-coordinate

For x=-2

substitute in the expression above and solve for y

36=(y-5)^2

square root both sides

`\begin{gathered} y-5=\pm6 \\ y=\pm6+5 \end{gathered}`

Values of y are

y=11 and y=-1

therefore

we have the coordinates of point B

(-2,11) and (-2,-1)

Find out the third possible coordinate of point B

I will assume the y-coordinate

For y=5

36=(x+2)^2

square root both sides

`\begin{gathered} x+2=\pm6 \\ x=\pm6-2 \end{gathered}`

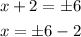
the values of x are

x=4 and x=-8

the possibles values of B are

(4,5) and (-8,5)

therefore

Possibles values of point B are

(-2,11)

(-2,-1)

(4,5)

(-8,5)

Part 2

Find out the midpoint of each of those possible segments

The formula to calculate the midpoint between two points is equal to

`M((x1+x2)/(2),(y1+y2)/(2))`

so

For A(-2,5) and B(-2,11)

substitute in the formula-------> M(-2,8)

For A(-2,5) and B(-2,-1) ------> M(-2,2)

For A(-2,5) and B(4,5) -------> M(1,5)

For A(-2,5) and B(-8,5) -----> M(-5,5)