Given:
Mean = 64.2
Standard deviation = 2.9 inches
Let's solve for the following:
• (a). What height represents the 95th percentile?
At the 95th percentile, the z-score is 1.645
Apply the z-score formula:

Where:
z = 1.645
μ = 64.2
σ = 2.9
Let's solve for x:
Rewrite the equation for x:
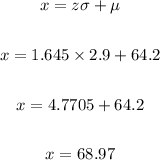
Therefore, the height that represents the 95th percentile is 68.97 inches.
• (b). , What height represents the first quartile?
We have:
The z-value for the height of the first quartile is:
P(Z < z) = 0.25
Using the standard normal distribution table, we have:
NORMSINV(0.25) = -0.67
z = -0.67
Now, apply the z-score formula:

Where:
z = -0.67
u = 64.2
σ = 2.9
Let's solve for x:
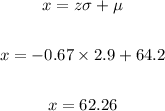
Therefore, the height that represents the first quartile is 62.26 inches.
ANSWER:
• (a). 68.97 inches
,
• (b). 62.26 inches