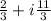Given:-
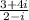
To find:-
The simplified form.
At first we take conjucate and multiply below and above.
The conjucate is,
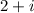
So now we multiply. we get,
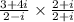
Now we simplify. so we get,
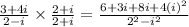
We know the value of,
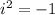
Substituting the value -1. we get,
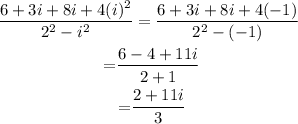
So now we split the term to bring it into the form a+ib. so we get,
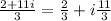
So the required solution is,