Question

I need the formula and how to solve it quickly.

Answer 1

Answers:

a. 8.7 m/s²

b. 10 N

c. 5 N

Step-by-step explanation:

The free-body diagram for the block is

Part (a)

By the second law of Newton, the net horizontal force is equal to mass times horizontal acceleration. In this case, the net horizontal force is the horizontal component of the tension, sp

Fnet = ma

Tx = ma

Tcos30 = ma

Solving for a, we get:

a = Tcos30/m

So, replacing T = 10N, cos 30 = 0.87 and m = 1.0 kg, we get:

a = 10(0.87)/1 = 8.7 m/s²

Therefore, the horizontal acceleration of the block, to one decimal place, is 8.7 m/s²

Part (b)

The weight of the block is equal to mass times gravity, so

W = mg

W = (1.0 kg)(10 m/s²)

W = 10 N

Then, the weight of the block is 10 N

Part (c)

The block is not accelerating in the vertical direction, so the net vertical force is 0 N, then

`\begin{gathered} Fn+T_y-W=0 \\ Fn+T\sin 30-W=0 \end{gathered}`

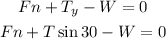
Solving for the normal reaction Fn, we get:

`Fn=W-T\sin 30`

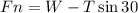
Replacing the weight W = 10N, T = 10N and sin30 = 0.5, we get:

`\begin{gathered} Fn=10N-10N(0.5) \\ Fn=10N-5N \\ Fn=5N \end{gathered}`

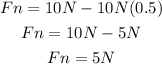
Therefore, the normal reaction is 5N