Question

A rose garden Is formed by jolning a rectangle and a semicircle, as shown below. The rectangle Is 23 ft long and 14 ft wide.Find the area of the garden. Use the value 3.14 for M, and do not round your answer. Be sure to include the correct unit in your answe

Answer 1

Area of the garden:

`\begin{equation*} 398.93\text{ ft}^2 \end{equation*}`

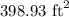
Step-by-step explanation:

Given the below parameters;

Length of the rectangle(l) = 23 ft

Width of the rectangle(w) = 14 ft

Value of pi = 3.14

Since the width of the rectangle is 14 ft, so the diameter(d) of the semicircle is also 14 ft.

The radius(r) of the semicircle will now be;

`r=(d)/(2)=(14)/(2)=7\text{ ft}`

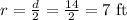
Let's now go ahead and determine the area of the semicircle using the below formula;

`A_(sc)=(\pi r^2)/(2)=(3.14*\left(7\right)^2)/(2)=(3.14*49)/(2)=(153.86)/(2)=76.93\text{ ft}^2`

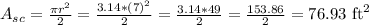
Let's also determine the area of the rectangle;

`A_r=l*w=23*14=322\text{ ft}^2`

We can now determine the area of the garden by adding the area of the semicircle and that of the rectangle together;

`\begin{gathered} Area\text{ of the garden = Area of semi circle + Area of rectangle } \\ =76.93+322 \\ =398.93\text{ ft}^2 \end{gathered}`

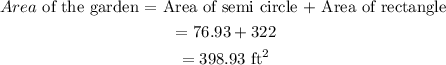
Therefore, the area of the garden is 398.93 ft^2