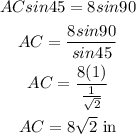Question

Can you help me with this? The other tutor couldn't help with this question

Answer 1

`AC=8√(2)\text{ in}`

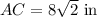
Explanations:

Given the sketch of the triangle shown below:

From the figure shown, the measure of the interior quadrilateral is 360 degrees

30 + 30 + 30 + reflex = 360

reflex angle = 360 - 90

reflex angle = 270 degrees

Since AB = BC = 8in

To determine the measure of AC, we will use the sine rule

`\begin{gathered} (AC)/(sin\angle ABC)=(BC)/(sin\angle BAC) \\ (AC)/(sin90)=(8)/(sin45) \\ \end{gathered}`

Simplify the result

`\begin{gathered} ACsin45=8sin90 \\ AC=(8sin90)/(sin45) \\ AC=(8(1))/((1)/(√(2))) \\ AC=8√(2)\text{ in} \end{gathered}`