Function 1:
The quadratic function is given as:
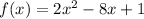
Factor out 2:
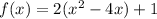
Rewrite the expression in the bracket, as follows:
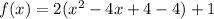
This gives:
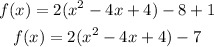
Express as a perfect square:
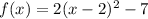
A quadratic function is represented as:

Where: vertex (h,k)
By comparison, we have:
Vertex = (2, -7)
This represents the minimum of function 1.
Function 2:
From the graph, the minimum of function 2 is:
Vertex = (-1, -3)
(2,-7) is lesser than (-1,-3)
Answer: Function 1 has the least minimum value at a coordinate of (2,-7)