Question

3 Done Exercise Set 4.3 (Chapter 21) 1. NOTE: The numerical values in this problem have been modified for testing purposes. Forests are complex, evolving ecosystems. For instance, pioneer tree species can be displaced by successional species better adapted to the changing environment. Ecologists mapped a large Canadian forest plot dominated by Douglas fir with an understory of western hemlock and western red cedar. Sapling trees (young trees shorter than 1.3 meters) are indicative of the future of a forest. The 242 sapling trees recorded in this sample forest plot were of the following types: Count of Samplings Tree Species Observed Expected Western Red Cedar 103 Douglas Fir 60 Western Hemlock 79 Can we conclude that there are equal proportions of saplings of these three species in this forest? Add the expected values to the table above. Compute the Chi-Square Goodness-of-Fit test: The value of Chi-Square = and p = (Give your answer to 4 decimal places) Can we conclude that there are equal proportions of saplings of these three species in this forest? O Yes O No

Answer 1

1) No

We cannot conclude that the sampling of these three species of this forest are of equal proportion because the difference between the observed values of any two of the sampled species is significant.

`\begin{gathered} P(x)=(x)/(242) \\ \text{and} \\ \text{ Expected value }=P(x)* x \end{gathered}`

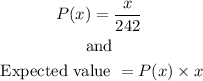
| Observed(x) | P(x) | Expected

--------------------------------------------------------------------------------------------------------

Western Red | 103 | 0.4256 | 43.8368

Cedar | | |

-------------------------------------------------------------------------------------------------------------

Douglas Fir | 60 | 0.2479 | 14.8740

----------------------------------------------------------------------------------------------------

Western | 79 | 0.3264 | 25.7856

Hemlock | | |

-------------------------------------------------------------------------------------------------------------

`\begin{gathered} X^2_c=\sum (\lbrack x-(xP(x))\rbrack^2)/(xP(x)) \\ \text{where} \\ X^2_(_c)=\text{ the Chi-Square Goodness of Fit } \end{gathered}`
`\begin{gathered} \text{Let} \\ A=x-xP(x),B=(A^2)/(xP(x)) \end{gathered}`

A | A² | B

--------------------------------------------------------------------------------------------------

59.1632 | 3500.2842 | 79.8481

-------------------------------------------------------------------------------------------

45.1260 | 2036.3559 | 136.9071

---------------------------------------------------------------------------------

53.2144 | 2831.7724 | 109.8199

-------------------------------------------------------------------------------

| ∑ = 326.5751

Therefore, the Chi-Square = 326.5751, p = 0