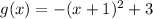IMAGE OF QUESTION
ANSWER
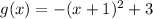
Step-by-step explanation
We have that the function graphed g(x) is a transformation of:
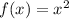
When the parent quadratic function f(x) is transformed, it takes the following form:

This form also represents the vertex form of a quadratic equation, where (h, k) is the vertex of the function.
This means that we can find the function by using the vertex of the function.
The vertex of a function is the maximum or minimum value of the function; from the given graph, it is a maximum value and it is located at:
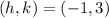
Therefore, we can input this into the vertex form of the function:
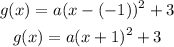
Now, we have to find the value of a. To do this, pick any coordinate point from the graph and input it into the function above.
Let us pick:
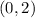
Therefore, we have:

Therefore, the function graphed above is: