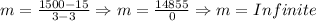We have the first function:
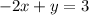
We solve for y, that is:
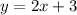
From the formula of a function of a line, we have:

Here m is the slope and b is the y-interceptm from this we have that from the first function the slope is equal to 2 and the y-intercept is equal to 3.
For the second function, we also solve for y, that is:
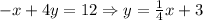
From this and the function of a line, we have that the slope equals 1/4 and the y-intercept equals 3.
The y-intercept of a function is the value of y when x=0, if for example the fucntion were:

It would still follow the rule:

The thing would be, that the slope in order to make the function true would be 1 and the y-intercept since x = 0 we will have that y=0, that in the rule would be:
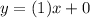
Now, the slope can be a fraction, or not a fraction, that is as per before y=x, the slope is again m = 1, and if it were to be put in a fraction notation we would have 1/1.
If the slope where just fractions, we would have that fucntions such as:
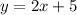
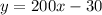
Wouldn't be possible, but we know that they are, since when we replace the different values of x and graph them they still show a line behavior.
By deffinition the slope is defined by the following:

Now, for say the following points that belong to a line (1, 1) and (2, 2), we would have:
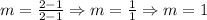
Now, the slope in this case would not be a fraction unless seen like this 1/1.
The slope can also be zero, if the line is a horizontal line, and the slope cannot be dfined [Or infinite] if the line is a vertical line, that is:
*Imagine a horizontal line, we would have points such as, (-10, 2) and (1000, 2), calculating the slope we would get:
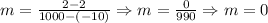
*Now, imagine a vertical line, we would have points such as (3, 15) & (3, 1500), then we calculate the slope: