1 Answer

Meneghino · Answer 1 · 2023-12-20T05:14:34+0000

We are asked to find the area of the target outside of the bullseye.

Recall that the area of a circular archery target is given by

$A=\pi r^2$

Where r is the radius.

The bullseye has a radius of 3 inches.

The area of the bullseye is given by

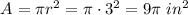
$A_{}=\pi r^2=\pi\cdot3^2=9\pi\; in^2$

The entire target has a radius of 9 inches.

The area of the entire target is given by

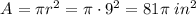
$A_{}=\pi r^2=\pi\cdot9^2=81\pi\; in^2$

Subtract the area of the bullseye from the entire target area to find the area of the target outside of the bullseye.

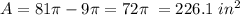
$A=81\pi-9\pi=72\pi\; =226.1\; in^2$

Therefore, the area of the target outside of the bullseye is 226.1 in^2

Option a. is the correct answer.

Please log in or register to add a comment.