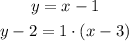The equation of line 'k' is given as,
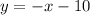
Consider that the slope-intercept form of a line having slope 'm' and y-intercept 'c' is given by,

On comparing, it can be claimed that the slope of line 'k' is,

Theorem: The product of slopes of two perpendicular lines is always -1.
Given that line 'l' is perpendicular to line 'k',

Then the equation of the line 'l' considering the y-intercept as 'C' is obtained as,
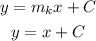
Given that the line 'l' passes through the point (3,2),
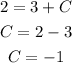
So the equation of the line 'l' in the slope-intercept form will be,
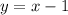
Consider that the point-slope form of a line is given by,
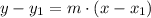
As discussed above, the slope of the line 'l' is 1, and it passes through the point (2,3),
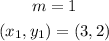
Then the corresponding equation of line 'l' in point-slope form, will be,
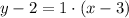
Thus, the equation of line 'l' in slope-intercept form and point-slope form respectively,