Question

Write an equation of a line that passes through the point (8, 4) and is parallel to the line y = 4x + 2. ay = 4x − 28 by = 4x + 28 cy = 1 over 4x − 2 dy = 1 over 4x + 2

Answer 1

a)y=4x-28

Step-by-step explanation

the equation of a line can be written as follows

`\begin{gathered} y=mx+b \\ where\text{ m is the slope} \\ and\text{ b is the y-intercept} \end{gathered}`

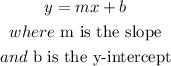
Step 1

a) find the slope of the given line

`\begin{gathered} y=4x+2\Rightarrow y=mx+b \\ hence \\ slope_1=4 \end{gathered}`

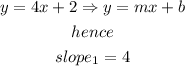
b)now, 2 lines are parallel it the slope is the same in both lines, so

the slope of the line we are looking for must be 4 as well

`\begin{gathered} slope_1=slope_2 \\ 4=slope_2 \end{gathered}`

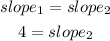
so

Slope = 4

Step 2

finally, use the slope -point formula to find the equation of the line

`\begin{gathered} slope-point\text{ formula} \\ y-y_1=m(x-x_1) \\ where\text{ m is the slope} \\ \text{ \lparen x}_1,y_1)\text{ is a point of the lines} \end{gathered}`

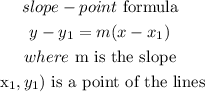
a) let

`\begin{gathered} point\text{ =\lparen8,4\rparen} \\ slope=\text{ 4} \end{gathered}`

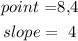
b) now, replace and isolate y

`\begin{gathered} y-y_(1)=m(x-x_(1)) \\ y-(4)=4(x-8) \\ y-4=4x-32 \\ add\text{ 4 in both sides} \\ y-4+4=4x-32+4 \\ y=4x-28 \end{gathered}`

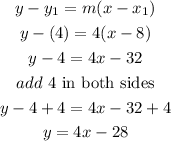
therefore, the answer is

a)y=4x-28

I hope this helps you