Question

The admission fee at a water park is $8.00 for children and &11.50 for adults. On a certain day, 321 people entered to park, and the admission fees collected totaled $3,173.50. How many children and how many adults were admitted? (This I’m confused about)

Answer 1

Hello!

First, let's write some important information contained in the exercise:

Fees:

• $8.00 for children

,

• $11.50 for adults

• On a certain day, ,321 people entered to park

,

• The admission fees ,collected totaled $3,173.50

Knowing that we can write it as a system, look:

`\begin{cases}8c+11.5a=3,173.50\text{ equation i)} \\ c+a=321\text{ equation ii)}\end{cases}`

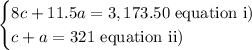
Let me explain the system:

Equation i) means that the total value obtained from the sale of tickets was $3,173.50.

Equation ii) means that the total of adults and children was 321 people.

Okay, now let's solve this system:

I will isolate the variable c in equation ii), look:

`\begin{gathered} c+a=321 \\ c=321-a \end{gathered}`

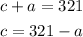
So from now on, we're going to use C = 321 - a.

Now, let's replace the value of C in the equation i):

`\begin{gathered} 8c+11.5a=3,173.50 \\ 8\cdot(321-a)+11.5a=3,173.50 \\ 2,568-8a+11.5a=3,173.50 \\ 2,568+3.5a=3,173.50 \\ 3.5a=3,173.50-2,568 \\ 3.5a=605.50 \\ a=(605.50)/(3.5) \\ a=173 \end{gathered}`

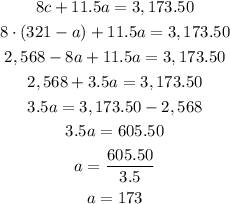
Now we know the number of adults as 173, let's replace it instead A in equation ii):

`\begin{gathered} c+a=321 \\ c+173=321 \\ c=321-173 \\ c=148 \end{gathered}`

According to the reasoning above, 148 children and 173 adults were admitted.