You have the following expression:
![f(t)=(5t^2+1)(2\sqrt[]{t}-3t+1)](https://img.qammunity.org/2023/formulas/mathematics/college/qyhtco06naptbrjw5chlckjzun8agx3r1q.png)
In order to derivate the previous function, notice that you have a product between two factors, then, by using the derivative of a product you obtain:
![f^(\prime)(t)=(5t^2+1)^(\prime)(2\sqrt[]{t}-3t+1)+(5t^2+1)(2\sqrt[]{t}-3t+1)^(\prime)](https://img.qammunity.org/2023/formulas/mathematics/college/8f1cq9pk5rdqbdiyx3wh0xd04wgiow2rbq.png)
Now, the derivatives of the factors are:
![\begin{gathered} (5t^2+1)^(\prime)=10t \\ (2\sqrt[]{t}-3t+1)^(\prime)=(2t^{(1)/(2)}-3t+1)^(\prime)=t^{-(1)/(2)}-3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yhaejk1sgx0d67u6biqchexvze7j53sato.png)
Then, by replacing the previous expressions into f'(t):
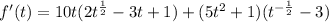
The previous expression is the result for the derivative of f(t).