Question

Suppose f is an exponential function where f(0)=4 and f(3)=6.912.What is the 3-unit growth factor for f?What is the 1-unit growth factor for f?What is the initial value of f?f(0)=Write a function formula for f.f(x)=

Answer 1

Considering the values of the exponential function:

`f(x)=ab^x`

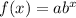
With values:

f(0)=4

f(3)=6.912

The initial value of the function f(x) is the value when x=0, in this case, the initial value is a=4

Using the initial value and the ordered pair (3,6.912) you can determine the growth factor (b)

`\begin{gathered} f(x)=4b^x \\ f(3)=4b^3 \\ 6.912=4b^3 \end{gathered}`

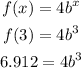
Divide both sides by 4

`\begin{gathered} (6.912)/(4)=(4b^3)/(4) \\ 1.728=b^3 \end{gathered}`

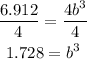
Apply the cubic square to both sides of the equal sign

`\begin{gathered} \sqrt[3]{1.728}=\sqrt[3]{b^3} \\ 1.2=b \end{gathered}`

The growth factor is b=1.2.

Now that the initial value and the growth factor of the function are determined you can write the equation of the function as follows:

`f(x)=4\cdot(1.2)^x`