Question

Suppose that the manufacturer of a gas clothes dryer has found that when the unit price is p dollars, the revenue R (in dollars) is R(p)= -2p^2+4,000p.A) At what prices p is revenue zero? B) For what range of prices will revenue exceed $400,000? Type answer in interval notation.

Answer 1

The quadratic equation models the revenue with respect to the unit price is:

`R(p)=-2p^2+4000p`

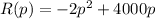
a) To find the prices when the revenue is zero, first zero the equation:

`-2p^2+4000p=0`

Using the quadratic equation, where "p" is the independent variable, normally represented with the letter "x"

`p=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where

a is the coefficient of the quadratic term, in this case, a= -2

b is the coefficient of the x-term, in this case, b= 4000

c is the constant of the quadratic equation, in this case, c= 0

`\begin{gathered} p=\frac{-4000\pm\sqrt[]{(4000)^2-4\cdot(-2)\cdot0}}{2(-2)} \\ p=\frac{-4000\pm\sqrt[]{16000000-0}}{-4} \\ p=\frac{-4000\pm\sqrt[]{16000000}}{-4} \\ p=(-4000\pm4000)/(-4) \end{gathered}`

Solve the sum and difference separately:

-Sum:

`\begin{gathered} p=(-4000+4000)/(-4) \\ p=(0)/(-4) \\ p=0 \end{gathered}`

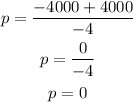
-Difference

`\begin{gathered} p=(-4000-4000)/(-4) \\ p=(-8000)/(-4) \\ p=2000 \end{gathered}`

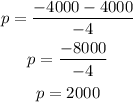
At the unit prices 0 and 2000, the revenue will be zero.

b) You have to find the values of p for which the revenue is equal to 400000, to do so, equal the quadratic equation to the given revenue value:

`400000=-2p^2+4000p`

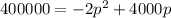
Zero the equation

`\begin{gathered} 400000-400000=-2p^2+4000p-400000 \\ 0=-2p^2+4000p-400000 \end{gathered}`

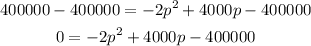
Use the quadratic equation to determine the prices, use:

a=-2

b=4000

c=-400000

`\begin{gathered} p=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ p=\frac{-4000\pm\sqrt[]{(4000)^2-4\cdot(-2)(-400000)}}{2\cdot(-2)} \\ p=\frac{-4000\pm\sqrt[]{16000000-3200000}}{-4} \\ p=\frac{-4000\pm\sqrt[]{12800000}}{-4} \\ p=(-4000\pm3577.708764)/(-4) \\ \end{gathered}`

Sum:

`\begin{gathered} p=(-4000+3577.708764)/(-4) \\ p=105.57 \end{gathered}`

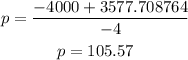
Difference:

`\begin{gathered} p=(-4000-3577.708764)/(-4) \\ p=1894.427\approx1894.43 \end{gathered}`

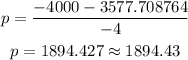
Between the prices $105.57 and $1894.43 the revenue will be greater than $400,000