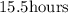Question

Approximating the equation of a line of best fit and making...VThe scatter plot shows the time spent watching TV, x, and the time spent doing homework, y, by each of 24 students last week.(a) Write an approximate equation of the line of best fit for the data. It doesn't have to be the exact line of best fit.(b) Using your equation from part (a); predict the time spent doing homework for a student who spends 15 hours watching TV.Note that you can use the graphing tools to help you approximate the line.

Answer 1

The picture below will really be of help

Note: The line is drawn based on the image sent and without the graphing tool

(a)

In order to find the approximate equation of the line of best fit

We have the two points from the line (8, 20) and (24, 8)

`\begin{gathered} Slope=(y_2-y_1)/(x_2-x_1) \\ Slope=(8-20)/(24-8) \\ Slope=(-12)/(16) \\ Slope=-(3)/(4) \end{gathered}`

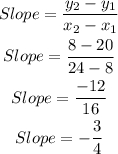
To get the equation

`\begin{gathered} y-y_1=m(x-x_1) \\ u\sin g\text{ (8, 20)} \\ y-20=-(3)/(4)(x-8) \\ y-20=-(3)/(4)x+6 \\ y=-(3)/(4)x+6+20 \\ y=-(3)/(4)x+26 \end{gathered}`

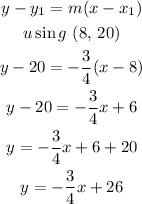
Therefore, the approximate line of best fit is

`y=-(3)/(4)x+26`

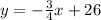
(b)

To find the part b, from the graph, the green line is to be traced to the y - axis

The approximate answer is

`15.5\text{hours}`