Question

Write an equation (a) in slope-intercept form and (b) in standard form for the line passing through (-3,5) and parallel to x + 2y = 5a) The equation of the line in slope-intercept form is   enter your response here.note: this question has two parts.

Answer 1

`\begin{gathered} a)y=-(1)/(2)x+(13)/(2) \\ b)(1)/(2)x+y=(13)/(2) \end{gathered}`

1) We need to rewrite that equation into the Slope-intercept form for a matter of convenience.

`\begin{gathered} x+2y=5 \\ 2y=5-x \\ y=(5-x)/(2) \\ y=(5)/(2)-(x)/(2) \end{gathered}`

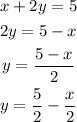
2) Now, we can properly work on what was told.

a) Since the point here is to find a parallel equation then we need to keep the same slope. So, our equation must have a slope equal to -1/2

Let's plug point (-3,5) into that:

`\begin{gathered} y=mx+b \\ 5=-(1)/(2)(3)+b \\ 5=-(3)/(2)+b \\ 5+(3)/(2)=b \\ (10)/(2)+(3)/(2)=b \\ b=(13)/(2) \end{gathered}`

Thus, this parallel line that passes through (-3,5) is:

`y=-(1)/(2)x+(13)/(2)`

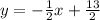
b) Let's rewrite it into the Standard form performing some algebraic manipulation adding 1/2x to both sides:

`(1)/(2)x+y=(13)/(2)`

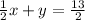
And those are the answers