Let us assume we are comparing these function to the function
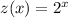
We can tell that function y will have an horizontal asymptote at y=6, because
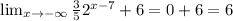
So we can discard the first option.
The function y is indeed displaced upward by 6 compared to z, but the horizontal displacement is 7 to the right since y(x)=z(x-7). Thus the second option is incorrect.
Since
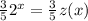
We can confirm that the function is compressed by a factor of 3/5.
It is not a reflection, and as we discussed earlier when calculating the limit of y as x tends to minus infinity, the domain is all the real numbers, but the function is always greater than 6, so its range is y >6.
Thus, the correct options are 3 and 5. Here's a graph of both functions to confirm our results: