Question

In a recent year, the scores for the reading portion of a test were normally distributed, with a mean of 22.4 and a standard deviation of 5.1. Complete parts (a) through (d) below.(a) Find the probability that a randomly selected high school student who took the reading portion of the test has a score that is less than 19.The probability of a student scoring less than 19 is(Round to four decimal places as needed.)(b) Find the probability that a randomly selected high school student who took the reading portion of the test has a score that is between 17.7 and 27.1.The probability of a student scoring between 17.7 and 27.1 is. -(Round to four decimal places as needed.)(c) Find the probability that a randomly selected high school student who took the reading portion of the test has a score that is more than 33.1.The probability of a student scoring more than 33.1 is(Round to four decimal places as needed.)(d) Identify any unusual events. Explain your reasoning. Choose the correct answer below.OA. None of the events are unusual because all the probabilities are greater than 0.05.OB. The event in part (c) is unusual because its probability is less than 0.05.OC. The events in parts (a) and (b) are unusual because its probabilities are less than 0.05.D. The event in part (a) is unusual because its probability is less than 0.05.Help me solve thisView an example

Answer 1

Given

In a recent year, the scores for the reading portion of a test were normally distributed, with a mean of 22.4 and a standard deviation of 5.1.

To find:

(a) Find the probability that a randomly selected high school student who took the reading portion of the test has a score that is less than 19.

(b) Find the probability that a randomly selected high school student who took the reading portion of the test has a score that is between 17.7 and 27.1.

(c) Find the probability that a randomly selected high school student who took the reading portion of the test has a score that is more than 33.1.

(d) Identify any unusual events. Explain your reasoning. Choose the correct answer below.

Step-by-step explanation:

It is given that,

In a recent year, the scores for the reading portion of a test were normally distributed, with a mean of 22.4 and a standard deviation of 5.1.

That implies,

a) Consider x=19.

Then,

`\begin{gathered} z=(x-\mu)/(\sigma) \\ =(19-22.4)/(5.1) \\ =-0.6667 \end{gathered}`

Therefore,

The probability of a student scoring less than 19 is,

`\begin{gathered} P(x<19)=P(z<-0.6667) \\ =0.25249 \\ =0.2525 \end{gathered}`

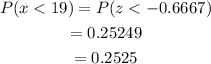
Hence, the probability of a student scoring less than 19 is 0.2525.

b) Consider x=17.7 and 27.1.

Then,

Hence, the probability of a student scoring more than 33.1 is 0.0180.

d) Since, a probability of 5%, or 0.05, is considered unusual.

Then, the unusual event is,

Option B),

The event in part (c) is unusual because its probability is less than 0.05.