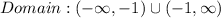ANSWER:
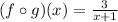
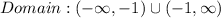
Step-by-step explanation:
Given:

To find (f o g)(x), we have to substitute x in f(x) with (x + 1)/3 and simplify as seen below;
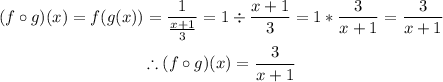
Recall that the domain of a function is the set of input values for which a function is defined.
So to determine the domain of the stated function, we have to equate the denominator to zero and solve for x as seen below;
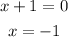
We can see that for the given function to be defined, x must not be equal to -1, so we can go ahead and write the domain of the function in interval notation as;