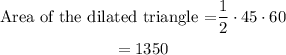The sides of the given triangle are 15,20 and 25.
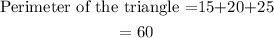
Find the area.
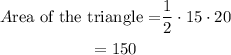
The length of the sides of the dilated triangle are 3 times the sides of the original triange.
So, the sides of the dilated triangle are:
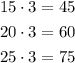
So, the perimeter of the dilated triangle is the sum of 45, 60 and 75.
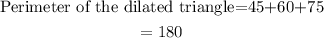
Now, find the area of the dilated triangle.