Question

Given the function z=2x +yFind the value objective at each corner of the graph

Answer 1

Given

Objective function

z=2x +y

Constraints

`\begin{gathered} 2x+3y\leq24 \\ x+y\ge2 \\ x\ge0,y\ge0 \end{gathered}`

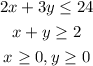
Find

a) Graph the system of inequality

b) Find the value objective at each corner of the graph

Step-by-step explanation

a) by using the graphing tool we graph the constaints.

2x + 3y = 24

if x = 0 then y = 8 ; (0 , 8)

if y = 0 then x = 12 ; (12 , 0)

x+y=2

if x = 0 then y = 2 ; (0 , 2)

if y = 0 then x = 2 ; (2 , 0)

here below is the graph

from the graph , the corner points are (0,2) ; (2 , 0) ; (12 , 0) and (0,8)

now , substitute these points to get the value of objective function .

for (0 , 2)

Z = 2x + y = 2(0) + 2 = 2

for (2 , 0)

Z = 2(2) + 0 = 4

for (12 , 0)

Z = 2(12) + 0 = 24

for (0 , 8)

Z = 2(0) + 8 = 8

Final Answer

Hence , the value of objective function at each corner is 2 , 4 , 24 , 8