Given:
The length of the arc PQ=12 cm
The angle of the sector POQ is 60 degrees.
To find the area of the sector and perimeter of the sector:
Using the length of an arc formula,
![\begin{gathered} l=(\theta)/(360)*2\pi r \\ 12=(60)/(360)*2*(22)/(7)* r \\ 12=(22)/(21)* r \\ r=(12*21)/(22) \\ r\approx11.455\operatorname{cm} \end{gathered}]()
Using the formula of area of the sector,
![\begin{gathered} A=(\theta)/(360)*\pi r^2 \\ =(60)/(360)*(22)/(7)*(11.455)^2 \\ =68.76\operatorname{cm} \end{gathered}]()
Therefore, the area of the sector is approximately 68.76 square cm.
Using the formula of the perimeter of the sector,
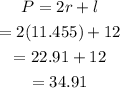
Therefore, the perimeter of the sector is approximately 34.91 cm.