Given the following System of equations:
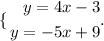
You can find the exact solution as following:
1. You can make both equation equal to each other:
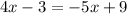
2. Now you must solve for the variable "x" in order to find its value. This is:
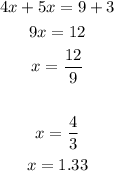
3. Substitute the value of "x" into any original equation and evaluate, in order to find the value of "y":
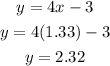
Then you get this solution written as an ordered pair:
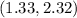
You can determine that the best approximation of the exact solution is: Option A.