C)
Step-by-step explanation
the weigth of a mass is given by the formula
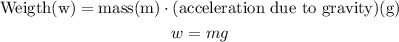
we already now, that the acceletion of gravity is bigger in the earth than in the moon ( because it depens on the mass, and the earth has very more mass than the moon)
so, for the moon we have
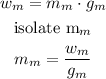
now, when the mass in in the earth
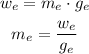
now, if we compare the masses ,equal ratios

we can see a ration of the weigth and g, as w depens on g, we can replace
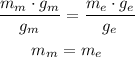
we can conclude mass is the amount of matter in an object and does not change with location
If an object is moved to a location of greater gravitational force, , its weight will increase, but mass still remains the same.
so, the answer is
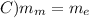
I hope this helps you