Question

Verify algebraically if the function is even, odd, or neither. Number nine

Answer 1

To determine if a function is even, odd or neither, we need to verify by the definition of an odd and even function, as follows:

Even function:

`f(x)=f(-x)`

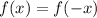
Odd function:

`g(-x)=-g(x)`

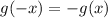
In the number 9, we have the following function:

`h(x)=|x|-1`

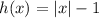
If we substitute the value from x to -x, we have the following:

`h(-x)=|-x|-1`

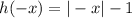
but, by definition, we have:

`|-x|=|-1* x|=|-1|*|x|=1*|x|=|x|`

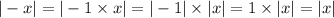
From this, we can rewrite the function h(-x) as follows:

`h(-x)=|-x|-1=|x|-1=h(x)`

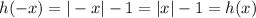
And from this, we can say that:

`h(-x)=h(x)`

And from the solution developed above, we are able to conclude that the function described by h(x) in number 9 is an even function