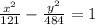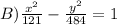
1) Considering that the vertices and co-vertices are: (11,0) and (-11,0) and (0,22) and (0,-22) we can visualize that this hyperbola has their arches passing through the x-axis.
2) We can then, write out the following to get the equation of the hyperbola:
![\begin{gathered} (\left(x-h\right)^2)/(a^2)-(\left(y-k\right)^2)/(b^2)=1 \\ h=0,k=0 \\ a^2=\left(k+11\right)^2\Rightarrow a=11 \\ b^2=\left(k-22\right)^2\operatorname{\Rightarrow}b=22 \\ \\ ((x-h)^(2))/(a^(2))-((y-k)^(2))/(b^(2))=1 \\ \\ ((x-0)^2)/(11^2)-((y-0)^2)/(22^2)=1 \\ \\ (x^2)/(121)-(y^2)/(484)=1 \end{gathered}]()
Note that this is the vertex form. So we can tell the answer is: