We are asked to determine the wavelength of a photon. To do that we will use the following formula:
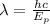
Where:

To calculate the change in energy of the photon we will use the following formula:
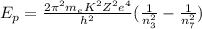
Where:

The mass of the electron is given by:
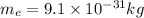
The electric constant is given by:
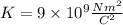
The atomic number of hydrogen is Z = 1.
The elementary charge has a value of:

Planks constant is equivalent to:
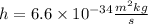
Now, we substitute the values:
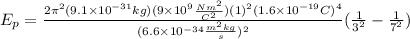
Solving the operations:
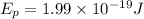
Now, we substitute the value in the formula for the wavelength:
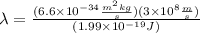
Solving the operation:
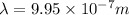
In nanometers the wavelength is:
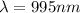
Therefore, the wavelength is 995 nanometers.