To answer this question, we can see that the function that gives the height of the weight at any given time is a parabola with a maximum (the negative number in front of the leading term gives us this information):
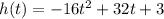
We can find the maximum height of the weight by finding the vertex of the parabola - we already know that this vertex is a maximum in this case.
The formula to find the vertex of a parabola is given by:

This is for the next general equation:

Now, we have that the parabola is:
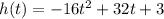
Then we have:
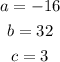
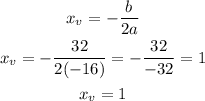
And
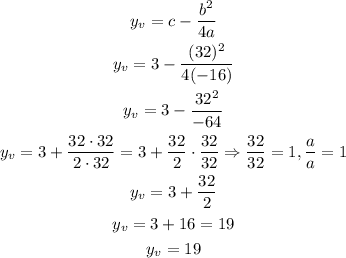
Therefore, we have that the vertex of the parabola is (1, 19). That is, we have that the maximum point for this parabola is y = 19 - this is the maximum value for the function, and the function takes this value when x = 1.
In other words, in summary, we have:
• The maximum height of the weight is 19 feet (we assume the function gives us the height in feet.)
,
• The weight will take 1 second to reach the maximum height (we assume that the function is expressed in seconds.)
,
• The contestant will not win a prize since the weight will never reach 20 feet.