Step 1: Write out the formula

Step 2: Find the time taken by A to travel 300miles.
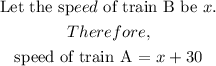
in this case,
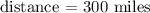
Therefore,
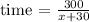
Step 3: Find the time taken by B to travel 180miles

Then
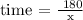
Step 4: Find x
Since the time A travels 300 miles is the same time B travels 180 miles, then
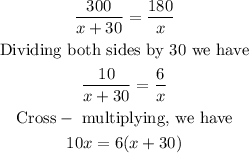
Expanding, we have
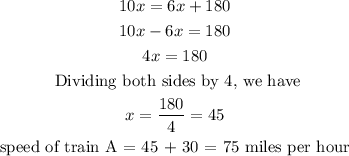
Therefore, the speed of train B is 45 miles per hour and that of train A is 75 miles per hour