We have the function:
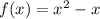
We have to find the vertex.
We can do it by rearranging the equation into vertex form:

We can do it like this:
The axis of symmetry, as this is a parabola for axis y, is a vertical line that pass through the vertex.
Vertical lines are defined as x=constant, and in this case, the vertical line that is the axis od fymmetry is x=0.5.
The x-intercepts of f(x) are the roots. We can calculate them in this case by factorizing the equation:

The x-intercepts are x=0 and x=1.
As the value of the quadratic coefficient is a=1 and is positive we know that we have a concave up parabola.
This means that in the vertex we have a minimum value for the function.
The value for this minimum is f(0.5)=-0.25.
The y-intercept is the value of f(x) when x=0. We can find it by replacing x with 0 and calculate f(x):
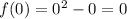
The y-intercept is y=0. We already know this point as it is a root of f(x).
Answer:
vertex: (0.5, -0.25)
axis of symmetry: x=0.5
x-intercept: x=0 and x=1
maximum or minimum: minimum
max/min value: y=-0.25
y-intercept: y=0