You have the following trinomial:
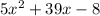
The general form of a trinomial is:
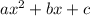
In order to find the factors you use the quadratic formula, which is given by:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
By comparing the given trinomial with the general form you have;
a = 5
b = 39
c = -8
You replace the previous values into the quadratic formula:
![\begin{gathered} x=\frac{-39\pm\sqrt[]{(39)^2-4(5)(-8)}}{2(5)} \\ x=\frac{-39\pm\sqrt[]{1521+160}}{10} \\ x=\frac{-39\pm\sqrt[]{1681}}{10}=(-39\pm41)/(10) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/21amu4uskb493scd71sv48hq1mxp9cgtby.png)
Then, you have the following two solutions:
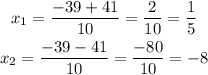
The factor of the trinomial are of the form:
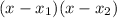
Finally, by replacing you obtain:
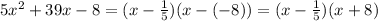
Hence, the factors are (x - 1/5)( x + 8)