The expression is given as,
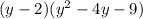
Consider the property of indices,
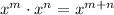
Use this property to resolve the given product,
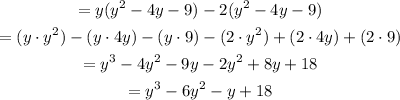
Thus, the simplified form of the given product of polynomial is obtained as,
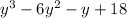
Since the highest integral exponent of the variable, 'y' in the expression is equal to 3.
Therefore, the degree of the obtained polynomial is also 3.
Thus, it can be concluded that -
The product simplifies to,
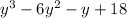
The degree of our simplified expression is 3.