Given the dimensions of the basket:
height = 20 inches
diameter = 12 inches
The radius of the basket will be:
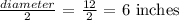
We know that the shape of a basket is a cylinder,
Thus, let's find the volume of the basket, using the formula:
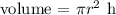
where,
h = 20 inches
r = 6 inches
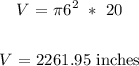
Now a golf ball has a diameter of approximately 1.68 inches
Now find the volume of the golf ball since it ia spherical in shape, using the formula:
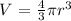
where radius of a golf ball, r = 1.68/2 = 0.84 inches
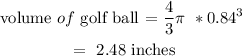
To find how many golf balls will fit into the basket, we have:
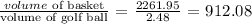
Therefore, we can see that approximately 912 golf balls will fit into the basket.
ANSWER:
912 golf balls