Question

Determine which theorem justifies the congruence of the triangles ABC and ADC.

Answer 1

First, we should remember the criteria for congruence of triangles: SSS (side-side-side), ASA (angle-side-angle), AAS (angle-angle-side) and SAS (side-angle-side).

First Angle

In the figure above, we know that the angles

`\begin{gathered} \measuredangle BAC\cong\measuredangle DCA \\ \cong\text{ means congruence} \end{gathered}`

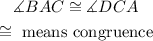
It means, that are congruent.

Second Angle

Also, the angles shown with a small square are right, and are congruent:

`\measuredangle DAC\cong\measuredangle BCA`

A side

At last, we know that the side AC belongs to both triangles, and it is congruent with itself (it means, its size is the same as the same segment).

We have then two angles and a side. As the side is between the to angles, we have the criteria SAS, and the triangles ABC and ADC are congruent.