Question

c) A surveyor in a boat on the river at point A was able to gather some information about the terrain arounda river. How far is it across the river (from B to C to the nearest foot), if the angle from the surveyor to thetwo points on the shore (BAC) was 13° and the angle from the shore at point B to the boat and the otherpoint on the shore (ABC) is 97° and the estimated distance from A to B is 75 ft?FANAB97⁰75 ft

Answer 1

17.95 ft

Step-by-step explanation:

First, we need to calculate the missing angle. The sum of the interior angles of a triangle is always equal to 180 degrees, so we can write the following equation

∠BCA + ∠BAC + ∠ABC = 180

∠BCA + 13 + 97 = 180

Solving for ∠BCA, we get:

∠BCA + 110 = 180

∠BCA + 110 - 110 = 180 - 110

∠BCA = 70

Now, we can use the sine Law to find the distance from B to C

`\begin{gathered} (BC)/(\sin(\angle ABC))=(AB)/(sin(\angle BCA)) \\ \\ (BC)/(\sin13)=(75)/(\sin70) \end{gathered}`

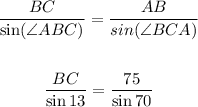
Solving for BC, we get

`\begin{gathered} BC=(75)/(\sin70)\cdot\sin13 \\ \\ BC=17.95\text{ ft} \end{gathered}`

Therefore, the answer is 17.95 ft