We need to substitute each point in the given equation and see if they fulfill the equality.
Case A)
By substituting point (7,5), we have
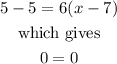
then, the point (7,5) belong to the line.
Case B).
By substituting point (5,7), we get
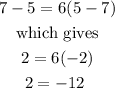
which is an absurd result. Then, point (5,7) does not belongs to the line
Case C)
By substituting point (-7,-5), we obtain
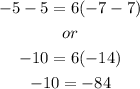
again, this is an absurd result, so this point does not belongs to the line.
Case D).
By replacing point (-5,-7), we have
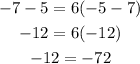
then, this point does not belongs to the line.
Therefore, the answer is option A.