![y=4\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/wdrgn9jw04pbx22pbe0mml8voi8v4be4bn.png)
Step-by-step explanation
the coordinate (0,y) makes a triangle
then
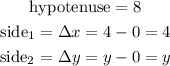
now, we can use the Pythagorean theorem to find y. P.T states that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse,so in this case.
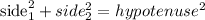
replace.
![\begin{gathered} \text{side}^2_1+side^2_2=hypotenuse^2 \\ 4^2+y^2=8^2 \\ 16+y^2=64 \\ y^2=64-16(\text{subtract 16 in both sides)} \\ y^2=48 \\ \text{square root in both sides} \\ y=\sqrt[]{48} \\ \text{apply properties of the root} \\ y=\sqrt[]{16\cdot3} \\ y=\sqrt[]{16}\cdot\sqrt[]{3} \\ y=4\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ryjff52mguazpx36slli1kb7uels2yjxvo.png)
therefore, a posible value for y is
![y=4\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/wdrgn9jw04pbx22pbe0mml8voi8v4be4bn.png)
I hope this helps you