Solve each equation first and then choose the appropiate statement.
Equation 1
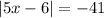
Since the absolute value of a number is always greater than 0 and -41<0, then this equation has no solutions.
Equation 2
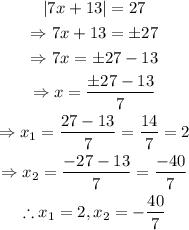
We can see that Equation 1 has 0 solutions and Equation 2 has 2 solutions.
Therefore, equation 2 has more solutions than equation 1.