Question

I need help with this question please. This is part of a practice homework help

Answer 1

Given the function:

`f(x)=3x^2-12x+1`

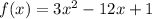
Let;s find the minimum or maximum value.

To determine if the function has a maximum or minimum, consider the following conditions:

• If the first term of the quadratic function is negative, the function has a maximum.

,

• If the first term of a quadratic function is positive, the function has a minimum.

Here, the first term is positive, therefore, the function has a minimum.

To find the minimum at x, apply the formula:

`x=-(b)/(2a)`

To determine the values of a and b, aply the general quadratic ecpression:

`ax^2+bx+c`

Now, compare both expressions:

`\begin{gathered} ax^2+bx+c \\ \\ 3x^2-12x+1 \end{gathered}`

Thus, we have:

a = 3

b = -12

c = 1

Hence, to find the minimum, substitute 3 for a, and -12 for b in the minimum formula above:

`\begin{gathered} x=-(b)/(2a) \\ \\ x=-(-12)/(2(3)) \\ \\ x=(12)/(6) \\ \\ x=2 \end{gathered}`

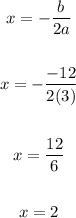
Now, to find the minimum, solve for f(2).

Substitute 2 for x in the function and evaluate for f(2):

`\begin{gathered} f(2)=3(2)^2-12(2)+1 \\ \\ f(2)=3(4)-24+1 \\ \\ f(2)=12-24+1 \\ \\ f(2)=-11 \end{gathered}`

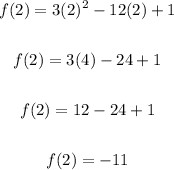
Therefore, the minimum of the function occurs at the point: (2, -11)

When x = 2, y = -11

ANSWER:

Minimum; -11