Question

Experts fear that without conservation efforts, an endangered species could disappear from the wild by 2022. Just one hundred years ago, there were at least 100,000 of this endangered species. By 2010, the estimated world population of this endangered species was 12,100. The bar graph shows the estimated world population of this endangered species for selected years from 1970 through 2010. Also shown is a polynomial function, with its graph, that models the data. Use this information to complete parts a through c.Polynomial model:f(x) = 0.72x³ - 23x² - 875x + 37821Continuation of part a:Identify this information as a point on the graph of f.b. Does f(4) overestimate or underestimate the actual data shown by the bar graph? By how much?c. Use the leading coefficient test to determine the end behavior to the right for the graph of f(x). Will this function be useful in modeling the population of this endangered species if conservation efforts to save this species fail? Explain your anwser

Answer 1

Looking at the polynomial model graph, we can see that the horizontal axis represents the number of years after 1970.

That means when the value in the horizontal axis is 40, it represents 40 years after 1970, that is, year 2010.

The value f(40) represents the world population 40 years after 1970.

To find the value of f(40), let's use x = 40 in the function f(x) and then calculate its value:

`\begin{gathered} f(x)=0.72x^3-23x^2-875x+37821 \\ f(40)=0.72\cdot40^3-23\cdot40^2-875\cdot40+37821 \\ f(40)=46080-36800-35000+37821 \\ f(40)=12101 \end{gathered}`

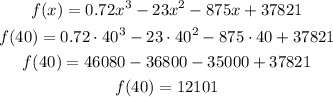
In order to represent this information as a point in the graph, we can use the notation (x, f(x)), where the value in the horizontal axis is x and the value in the vertical axis is f(x).

Since x = 40 and f(x) = 12101, we have the point (40, 12101).

b.

Looking at the bar graph, the value of the estimated world population for year 2010 is equal to 12100.

The value we calculated in the polynomial model is 12101, therefore the polynomial function overestimates the population size by 1 when compared to the bar graph.

c.

Looking at the leading coefficient of the polynomial, it's a positive value. That means when x tends to positive infinity (to the right of the graph), the value of f(x) will tend to positive infinity (values of f(x) will be increasing).

If the efforts fail, the population should decrease, and since the function will increase instead, it will not be useful.

Therefore the answer is:

The graph will rise to the right, and thus will not be useful if the population of this endangered species continues to fall.