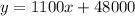Question

The population of the FreeTheMount neighborhood has been growing steadily since 1986. In 1988, the population was 50200 people. In 2000, it was 63400 people. Find an equation in the form y=mx+b, where x is the number of years past 1986 and y is the population of FreeTheMount. Answer:y=_______Do not use commas in your answer

Answer 1

The equation of a line is given as:

`y-y_1=m(x-x_1)`

where m is the slope and (x1,y1) is a point through the line. The slope is given as:

`m=(y_2-y_1)/(x_2-x_1)`

In this case we have the points (since 1986) (2,50200) and (14,63400), then the slope is:

`\begin{gathered} m=(63400-50200)/(14-2) \\ m=(13200)/(12) \\ m=1100 \end{gathered}`

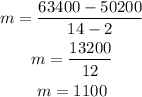
Plugging the values we have the equation:

`\begin{gathered} y-50200=1100(x-2) \\ y-50200=1100x-2200 \\ y=1100x+50200-2200 \\ y=1100x+48000 \end{gathered}`

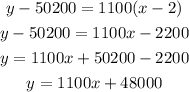
Therefore the equation we are looking for is:

`y=1100x+48000`