Final answer:
To maximize the space for the sheep, the farmer should make the two sides adjacent to the brick wall as long as possible. The dimensions that maximize the space are 30m by 15m.
Step-by-step explanation:
To maximize the space for the sheep, the farmer should make the two sides adjacent to the brick wall as long as possible. Let's call these sides x and y. Since the total length of fencing material is 60m, we can write the equation: x + 2y = 60. To find the dimensions that maximize the space, we need to maximize the area. The area of the pen is A = xy.
Solving the equation x + 2y = 60 for x, we get x = 60 - 2y. Substituting this value into the equation for the area, we have A = (60 - 2y)y = 60y - 2
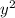 .
.
To find the maximum value of A, we can take the derivative of A with respect to y and set it equal to zero. Let's find the derivative: dA/dy = 60 - 4y. Setting this equal to zero and solving for y, we get y = 15. Substituting this value back into the equation x = 60 - 2y, we find x = 30.
Therefore, the dimensions that maximize the space for the sheep are 30m by 15m.