Question

Given the graph of the function f(x) = 2x2 + 5x − 33, use the Remainder Theorem to find the zeros of f(x).

Answer 1

`3,-(11)/(2)`

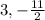
Step-by-step explanation:

Here, we want to get the zeros of the given function

According to the theorem, if we divide the polynomial by a linear factor, the remainder is given as substituting the roots into the function

With respect to the theorem, a linear factor is expected to have zero as its remainder

So,if we susbtituted the value in a linear factor into the polynomial, the remainder is zero

A root or zero of a function has a remainder equal to zero

In the given graph, we have the x-axis crossed at x = 3 and x = -5.5

It is expected that f(x) of these values will be zero

Let us make the substitution

We have this as follows:

`\begin{gathered} f(3)=2(3)^2+5(3)-33\text{ = 18+15-33 = 0} \\ f(-5.5)=2(5.5)^2+5(-55)\text{ - 33 = 0} \end{gathered}`

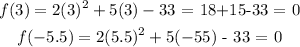
It can be seen from here that the roots are x = 3 and x = -11/2