To solve this question, follow the steps below.
Step 01: Create an equation such that x equals the decimal number.
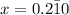
Let this equation be equation 01.
Step 02: Create a second equation by multiplying both sides of equation 01 by 10³.
We multiply both sides by 10³ since the decimal has 3 repeating numbers.
Since 10³ = 1000:
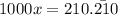
Let this equation be equation 02.
Step 03: Subtract equation 01 from equation 02.
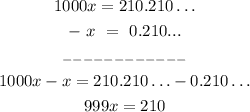
Step 04: Divide both sides of the equation by 999 to find x.
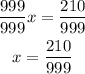
Simplify the fraction by dividing both the numerator and the denominator by 3.

Since
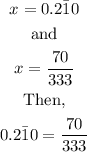
Answer:
