Question

5. Find the equation of theline:through:(-1,2), perp. to Y=1/3x+1

Answer 1

The line perpendicular to y = 1/3x + 1 has its slope as a negative inverse of the other one. The slope of the line given is 1/3 (the coefficient of x), therefore the slope of a perpendicular line is -3/1 or just -3. Since the point which it passes through has been given as (-1, 2), then;

`\begin{gathered} y=mx+b \\ \text{Substitute for the given values, x, y and the slope} \\ 2=-3(-1)+b \\ 2=3+b \\ 2-3=b \\ b=-1 \end{gathered}`

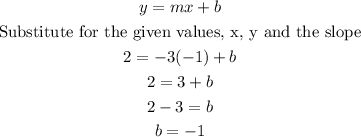
Having determined the y-intercept and the slope of the perpendicular line, the equation of the other lie can be written as;

`\begin{gathered} y=mx+b \\ y=-3x-1 \end{gathered}`

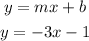
The equation of the line is therefore;

y = -3x - 1