Question

What is the probability of landing on a 4 and then landing on a 7

Answer 1

Probability

Let's say:

A: landing on a 4

B: landing on a 7

We have that the probability of each event is:

P(A) = 1/4

P(B) = 1/4

because it would be 1 out of four events.

Since they are independent events ( this means that it doesn't matter if we land on a 4 before, it will not affect the next result), the probability of landing on a 7 and landing on a 4 is given by

`\begin{gathered} P\mleft(AandB\mright)=P(A)\cdot P(AB) \\ P\mleft(AandB\mright)=(1)/(4)\cdot(1)/(4) \\ P(AandB)=(1)/(16) \end{gathered}`

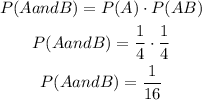
When the events are independent they both happening has a probability given by the product of each probability

Answer: P(AandB) = 1/16